薛定谔方程的定义

        薛定谔方程，有时也称为薛定谔波动方程，是一个偏微分方程。它使用能量守恒的概念（动能 + 势能 = 总能量）来获取有关绑定到原子核的电子行为的信息。它通过允许一个做到这一点电子的波函数，Ψ，来计算的。

求解薛定谔方程可以得到Ψ和Ψ 2。有了这些，我们可以获得量子数以及表征原子或分子中电子的轨道的形状和方向。

薛定谔方程只对具有一个电子的原子核给出精确解：H, He + , Li 2+ , Be 3+ , B 4+ , C 5+等。在数学语言中，我们说Ψ 的解析解是唯一可能的对于单电子系统。单电子系统通常被描述为氢的——意思是“像氢”。

对于所有其他原子、离子和分子，不可能有Ψ 的解析解；然后使用近似计算方法，例如轨道近似和变分定理。

有一个与时间相关的薛定谔方程和一个与时间无关的薛定谔方程。

时间无关方程认为电子的量子态是不变的，因此将电子视为驻波。与时间无关的方程允许使用波函数的平方Ψ 2找到电子密度（即原子和分子轨道的大小和形状）。

下面的 p 轨道是Ψ 2 的例子：

与时间无关的薛定谔方程

与时间无关的薛定谔方程可以用高度压缩的数学速记表示为：

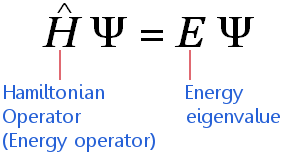
该方程适用于以非相对论速度运动的电子。（这意味着它需要在应用高质量元素之前进行调整。）等式表示：

与时间无关的方程可以写在任何合适的坐标系中，例如笛卡尔坐标 (x,y,z)。对于氢原子，球形极坐标更合适，因此：

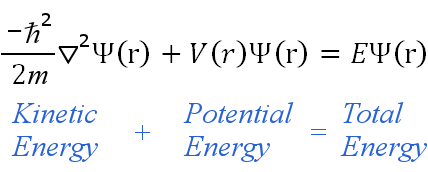
约束导致量化

求解方程以找到Ψ。求解方程的约束会产生量化——即为Ψ找到的解被限制为某些值，而所有其他值都被禁止。

这些限制是：

• Ψ及其一阶偏导数必须是连续的。

• Ψ必须是可归一化的：这意味着电子存在于宇宙某处的概率为 100%。对于实值Ψ，归一化要求：

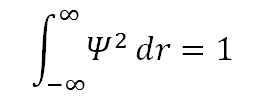
•随着与原子核距离的增加，电子分离并不再受束缚。即如 r → ∞, H → H + + e –。

波函数产生量子数

电子的波函数存在于三个维度中，因此薛定谔方程的解分为三个部分。这些是通过求解称为分离变量的偏微分方程的方法明确获得的。这样做，我们得到：

事实证明，Ψ 的解只有在以下情况下才有可能：

•在 R(r) 中，一个常数，称为 n，具有值 1、2、3、4……

•在 P(θ) 中，一个常数，称为l，具有值 0, 1, 2, 3,…(n-1)

•在 F(φ) 中，一个常数，称为m